Si pensamos en ‘informática’, seguramente vengan a nuestra cabeza imágenes de código pasando a gran velocidad, un futuro en el que la inteligencia artificial nos ayuda o increíbles imágenes renderizadas, tan realistas que no podemos distinguirlas de la propia realidad. Pero para que todo esto ocurra, los ordenadores tienen que ocuparse también de tareas más pedestres. De hecho, las Ciencias de la Computación no son sino el estudio de todas esas subtareas que subyacen en cualquier algoritmo, simple o avanzado. De todas ellas, nos ocuparemos de cómo consigue un ordenador hacer tan rápidamente algo que a cualquier niño le resulta tan pesado: ordenar.

Curiosamente, dentro del término ‘ordenar’ se esconden dos significados que requieren formas de proceder muy distintas. La primera es la versión más llana de ordenar: recibir un montón de datos y ponerlos en una secuencia siguiendo un patrón dado. Por ejemplo, si recibimos un montón de exámenes y queremos ordenarlos por orden alfabético de apellidos. El problema cambia si lo que queremos es mantener ordenado algo durante el tiempo. Pensemos por ejemplo en una biblioteca, donde todos los libros siguen ya un orden. Cuando llega una nueva remesa de libros, los bibliotecarios se encargan de ponerlos en su sitio, respetando el orden que ya había. Este segundo problema ocurre mucho más habitualmente en un ordenador (por ejemplo, las bases de datos suelen guardarse ya ordenadas) que en la vida real, donde el caos tiende a adueñarse de todo en cuanto le das una oportunidad.
En este artículo nos ocupamos del primer problema. El escenario es siempre el mismo: un ordenador recibe un montón de datos, y sabe por cada par de datos cuál tiene que ir antes en la fila que el otro. Este segundo elemento es una forma de abstraernos del problema; tanto da si ordenamos números, o si ordenamos personas por apellido, lo importante es conocer qué elementos “van antes” que otros. El resultado ha de ser siempre una secuencia de los mismos elementos, pero ordenados correctamente. Lo fascinante es que para un problema tan sencillo de explicar hay no uno, ni dos, sino decenas de algoritmos. En este artículo vamos a explicar algunos de ellos.
Pasito a pasito se hace camino
Los dos primeros algoritmos de los que nos ocupamos tratan al conjunto de datos de entrada elemento a elemento. Esto es, van escogiendo a casa paso uno de los valores que quieren ordenarse y haciendo algo con él. Como veremos después, esta no es la forma más eficiente de hacerlo, pero sí la más sencilla.
Empecemos por ‘minsort’, nombre que viene de ‘minimum sort’ o en castellano ‘ordenación por mínimos’. La idea es ir obteniendo a cada paso el mínimo elemento del conjunto que nos queda por ordenar, y añadirlo a la lista ya ordenada. Como cada vez en el conjunto a ordenar sólo quedan elementos “mayores”, esto nos garantiza que al final tenemos una secuencia ordenada.
Vamos a ver un ejemplo con los elementos “3, 2, 4, 1, 5”. ‘Minsort’ ejecuta 5 pasos hasta llegar a la lista ordenada:
- Busca el elemento mínimo, en este caso el 1, y lo pone como primer valor ya ordenado. Los elementos restantes son ahora “3, 2, 4, 5”.
- Se busca ahora el nuevo elemento mínimo, que es el 2, y se pone al final de la lista que ya teníamos, que pasa a ser “1, 2”. Los elementos restantes son “3, 4, 5”.
- El nuevo elemento mínimo es el 3, la lista ordenada es “1, 2, 3” y restan “4, 5”.
- En el penúltimo paso seleccionamos el 4, que pasa al final de la lista “1, 2, 3, 4”.
- Ya solo resta el número 5, así que la lista acaba siendo “1, 2, 3, 4, 5”.
Una apreciación importante es que aunque tras el paso 2 nuestro conjunto a ordenar estaba en realidad ordenado, el algoritmo no es capaz de “darse cuenta” de este hecho (y nosotros tampoco seríamos capaces si ese conjunto hubiese estado formado por 1000 en vez de por 3 elementos).
‘Minsort’ siempre da tantos pasos como elementos a ordenar
En la misma familia de algoritmos encontramos ‘insertion sort’, en castellano ‘ordenación por inserción’. En este caso también vamos incrementando una lista ya ordenada, pero en vez de elegir cada vez el mínimo elemento, lo que hacemos es escoger correctamente la posición de cada elemento a considerar. Por ejemplo, si tenemos la lista “a, c” y queremos insertar la letra “b”, nos encargamos de que la lista resultante sea “a, b, c”. Veamos nuestro ejemplo “3, 2, 4, 1, 5” ordenado por inserción:
- El primer elemento a considerar es el 3, con el que inauguramos nuestra lista ordenada.
- Luego cogemos el 2, que hemos de insertar en la lista con el 3. El algoritmo observa que 2 va antes que 3, por lo que la lista ordenada resultante es “2, 3”.
- Turno del número 4. El algoritmo pasa la posición de cabeza, puesto que 4 es mayor que 2, y también la posición intermedia, puesto que 4 es mayor que 3. El resultado, una nueva lista “2, 3, 4”.
Así continuamos con todos los elementos, hasta que la lista acaba siendo “1, 2, 3, 4, 5”, como era de esperar.
Una propiedad importante de los algoritmos, sea cual sea su finalidad, es cuántos pasos ha de dar para realizar su función. Esto es lo que llamamos la complejidad del algoritmo, y es una de las áreas fundamentales de estudio en Computación. En el caso de ‘minsort’, a cada paso hemos tenido que buscar el elemento mínimo; esto nos lleva tantas comparaciones entre elementos como elementos quedan. Por tanto, nuestro ejemplo toma 5 + 4 + 3 + 2 + 1 = 15 pasos. En general, si tenemos n elementos a ordenar, necesitamos n * (n + 1) / 2 pasos (lector o lectora, puedes comprobar que si n es 5, el resultado es el dado). Calcular la complejidad de ‘insertion sort’ es más complicado, puesto que depende de cuánto de la lista ya ordenada tengamos que “atravesar” para encontrar la posición. Sin embargo, el resultado en media es el mismo que ‘minsort’.
Podemos hacerlo mejor: podemos encontrar algoritmos que ordenen de forma más eficiente. Este no es un asunto baladí: menos tiempo de ordenación significa menos tiempo de espera para los usuarios. Y menos tiempo significa también menor consumo de energía: más tiempo para disfrutar del móvil en el tren, y menos emisiones.
Divide y vencerás
El problema con los anteriores algoritmos es que se intenta que funcione de forma global, es decir que ordenen de forma local, en otras palabras tratando cada elemento por separado. Nuestra siguiente tanda de algoritmos se encargan de dividir el conjunto inicial en diversos subconjuntos que se tratan por separado. De ahí que hablemos de algoritmos “divide y vencerás”, recordando la máxima romana.
Comencemos por ‘merge sort’, que podemos traducir como ‘ordenación por mezcla’, aunque en este caso la palabra ‘mezcla’ toma un cariz técnico y se refiere a una forma concreta de unir cosas. Pero no nos adelantemos. ‘Merge sort’ trabaja en dos fases: primero divide el conjunto inicial en mitades, y esas mitades en mitades, y así sucesivamente hasta acabar con conjuntos de un solo elemento.
En nuestro ejemplo, dividimos “3, 2, 4, 1, 5” en “3, 2, 4” y “1, 5” (que uno de los conjuntos sea más largo que otro es inevitable cuando ordenamos conjuntos con un número impar de elementos). Luego “3, 2, 4” se divide en “3, 2” y “4”, y por otro lado “1, 5” se divide en conjuntos de un solo elemento. Finalmente, “3, 2” se vuelve a dividir para alcanzar el objetivo de conjuntos de un solo elemento. Podemos visualizar este proceso como un árbol (o al menos, como lo que los informáticos entienden por árbol):
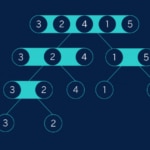
La segunda fase de ‘merge sort’ consiste en recomponer la lista, pero asegurándonos de que a cada paso está ordenada. La primera apreciación es que una lista de un sólo elemento siempre está ordenada. La segunda apreciación es que si tenemos dos listas que ya están ordenadas podemos unirlas fácilmente recorriéndolas en paralelo y eligiendo en cada momento el elemento menor de las dos listas. Este procedimiento es lo que llamamos técnicamente mezclas (merge) un par de listas ordenadas
En nuestro caso, comenzamos por las dos listas “3” y “2”. Mezclarlas produce la lista “2, 3”. Ya hemos considerado todas las listas de ese nivel, así que vamos al nivel superior en el árbol. Primero tenemos la lista “2, 3” (la versión ordenada de “3, 2”) y “4”, que al mezclar se convierten en “2, 3, 4”. Por el otro lado obtenemos “1, 5”. Finalmente tenemos que mezclar las listas “2, 3, 4” y “1, 5”. Todo este proceso se puede observar como el “reverso” de la fase de separación:
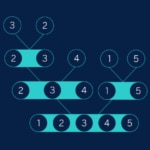
La gracia de todo esto es que los subconjuntos a ordenar se van haciendo exponencialmente más pequeños: a cada paso dividimos el conjunto por la mitad. Matemáticamente, vemos que el número de ‘niveles’ que tenemos en el árbol es el logaritmo en base 2 del número inicial de elementos. Como pequeño recordatorio, el logaritmo en base 2 de n es el número tal que 2 elevado a ese número da el n original. Por ejemplo, el logaritmo en base 2 de 8 es 3, puesto que 2 al cubo es exactamente 8. Como en cada nivel tenemos que mezclar tanto elementos como teníamos al principio, al final obtenemos que la complejidad de merge sort es n * log_2 n. No importa tanto el número concreto como el hecho de que es menor que en los dos algoritmos anteriores.
La forma de dividir elementos en ‘merge sort’ es bastante sencilla: la mitad para cada lado. Pero existe otra forma de hacerlo, y eso es lo que explota el algoritmo ‘quick sort’ (que se traduce como ‘ordenación rápida’). Lo que podemos hacer un elemento del montón a ordenar (esta elección acaba siendo irrelevante), y separar aquellos elementos que son menores que éste de aquellos que son mayores.
En nuestro ejemplo, “3, 2, 4, 1, 5”, vamos a escoger el elemento central como separador. En un primer paso este elemento es el 4, así que dividimos los elementos entre los menores que éste (3, 2, 1) y los mayores que éste, el 5. Ahora hacemos lo mismo con “3, 2, 1”: consideramos el 2 como elemento central y separamos los menores (1) de los mayores(3). Visualicemos este proceso en un árbol:

La gracia está en que ahora no necesitamos una segunda vuelta de mezcla: si leemos los elementos que están en los niveles más profundos del árbol ¡obtenemos la lista directamente ordenada! La única dificultad está en que ahora no tenemos que recordar solamente la división, sino también el elemento central.
Haciendo una cuenta un poco más compleja que en el caso de ‘merge sort’, obtenemos una complejidad similar. ¿De dónde viene el ‘rápida’ del nombre, pues? Resulta que si tomamos en consideración otras variables del algoritmo, como el uso de memoria, o el trasiego de copia de datos, ‘quick sort’ resulta mucho mejor en la práctica que ‘merge sort’. No obstante, ese análisis solo es válido si ejecutamos el algoritmo secuencialmente; si podemos dividir el trabajo en varios procesadores paralelos, merge sort vuelve a ser un buen contrincante. En todo caso, cuando de ordenar se habla, la mayor parte de los programadores acaba usando ‘quick sort’ o una variante del mismo.
Haciendo montoncitos
Imaginemos ahora lo siguiente: te damos un montón de pasaportes y te pedimos que los ordenes por número (y supongamos que el número de pasaporte es realmente un número, no un amasijo de letras y dígitos). ¿Qué es lo que harías?
Seguramente nada parecido a lo que hemos descrito hasta ahora. No: empezarías haciendo un montón con todos los pasaportes cuyo número empieza por 1, otro con los que empiezan por 2, y así sucesivamente (y si eres como yo, te darás cuenta al final que necesitas otro montón para los que empiezan por 0). Luego cogerías el montón del 1, y repetirías el proceso con la segunda cifra, y así sucesivamente hasta acabar con montones de un sólo pasaporte (o tener montones pequeños que puedes ordenar a simple vista). Felicidades, has ejecutado un algoritmo sin saberlo: ‘radix sort’, u ‘ordenación por raíz’.
Sin haber hecho ningún estudio contrastado, parece que esta es la forma más ‘natural’ de ordenar que tenemos los seres humanos. Sin embargo, este algoritmo se usa muy poco en programación. La razón es que nosotros ‘vemos’ un número como una serie de dígitos, de forma natural 41 es primero un 4 y luego un 1. Para un ordenador un número es un ente completo e indivisible: si queremos replicar lo que hemos hecho con los pasaportes en un ordenador nos llevará bastante trabajo obtener “la primera cifra del número”. Aparte de todo esto, para nosotros es sencillo hacer 10 montones, porque tenemos muy interiorizado el orden de los dígitos. Pero un ordenador ve los números compuestos por 1s y 0s, por lo que lo que “tendría más sentido” es hacer 2 montones. Así que volvemos a ‘merge’ o ‘quick sort’.
¿Se puede hacer mejor?
Las Ciencias de Computación tienen mucho de Matemáticas. En particular, al contrario que en Física o Química, en informática sí que podemos probar teoremas ciertos en cualquier situación, no simplemente hipótesis a contrastar en la naturaleza. Uno de esos teoremas nos dice que no podemos mejorar sustancialmente el tiempo que nos toma ordenar cosas más allá de ‘merge’ o ‘quick sort’.
Pero, ¡ojo!, este teorema es cierto solo para nuestro problema inicial. Si podemos asumir que parte del conjunto ya está ordenado, como en el caso de insertar un elemento en una base de datos, podemos hacerlo mejor. Y en toda esta discusión estamos asumiendo un ordenador convencional, capaz de realizar una sola operación al tiempo. Esta barrera puede que se esfume una vez la computación cuántica esté al alcance de todos.